Transition post-quantique : L’hybridation des échanges de clés

De manière plus urgente que pour les schémas de signature numérique, la façon dont nous échangeons des secrets partagés sur internet doit faire sa transition vers l’ère post-quantique. Cependant, en raison d’un recul relativement insuffisant concernant les nouveaux schémas d’échange de clés « post-quantiques », la plupart des institutions encouragent l’utilisation de schémas hybrides. Ces derniers combinent la robustesse de schémas classiques renommés avec la protection post-quantique offerte par les nouveaux schémas. Cet article de blog détaille l’état des lieux des principaux concepts d’échanges de clés hybrides.

Brefs rappels et définitions

Mécanismes d’encapsulation de clé (KEM)

Un Mécanisme d’encapsulation de clé (KEM) n’est qu’une façon sophistiquée de désigner une solution générique à un problème bien connu : comment Alice et Bob peuvent-ils partager un secret sur un canal public ? En cryptographie classique, ce problème est résolu par un échange de clés de type Diffie-Hellman : Alice et Bob publient leurs clés publiques respectives, et combinent leur clé privée avec la clé publique de l’autre pour aboutir à la même valeur secrète, qu’eux seuls peuvent connaître. En cryptographie post-quantique, diverses techniques existent pour établir ce secret partagé, dont certaines ont été abordées dans un article précédent sur les schémas basés sur les réseaux euclidiens1.

Un mécanisme d’encapsulation de clé est défini par trois algorithmes :

• KeyGen(), responsable de la génération d’une paire de clés, composée d’une partie privée et d’une partie publique.
• Encaps(Kpub), responsable de la génération d’un secret partagé et d’une « capsule ». Cette dernière est un blob binaire qui ne peut être retransformé en la valeur secrète que par le détenteur de la clé privée associée.
• Decaps(Kpriv, caps), utilisé pour récupérer le secret partagé à partir de la capsule, en utilisant la clé privée correspondante.

Par exemple, un échange de clés Diffie-Hellman (DH) classique peut être vu comme un KEM, en définissant les trois algorithmes de la manière suivante :

Paramètre public : un générateur g

• KeyGen() : Tirer un entier aléatoire s. Retourner K_priv = s et K_pub = g ** s
• Encaps(K_pub) : échange de clés Diffie-Hellman éphémère. Commencer par tirer un entier aléatoire x, puis calculer la clé publique associée qui servira de capsule caps = g ** x, et le secret partagé secret = K_pub ** x
• Decaps(caps, K_priv) : calcule simplement l’échange de clés entre la clé publique éphémère (la capsule) et la clé privée. secret = caps ** K_priv

Hybridation

L’hybridation est la pratique qui consiste à combiner des schémas post-quantiques et classiques pour obtenir un nouveau schéma, plus résilient, à la fois contre les attaques classiques et quantiques. Pour davantage de détails, une définition plus complète a déjà été abordée dans notre article de blog précédent sur l’hybridation des signatures. Nous vous encourageons à le lire, si ce n’est pas déjà fait2.

Combiner des mécanismes d’encapsulation de clé

Les combineurs de KEM ont été étudiés en profondeur par F. Giacon, F. Heuer et B. Poettering dans un article de 20183. Dans cet article, ils présentent une construction générique pour les combineurs, où tous les échanges de clés sont effectués en parallèle. Le travail de combinaison à proprement parler est réalisé à la fin, sous la forme d’une fonction W de tous les secrets partagés, capsules et clés publiques, qui produit en sortie le secret partagé combiné

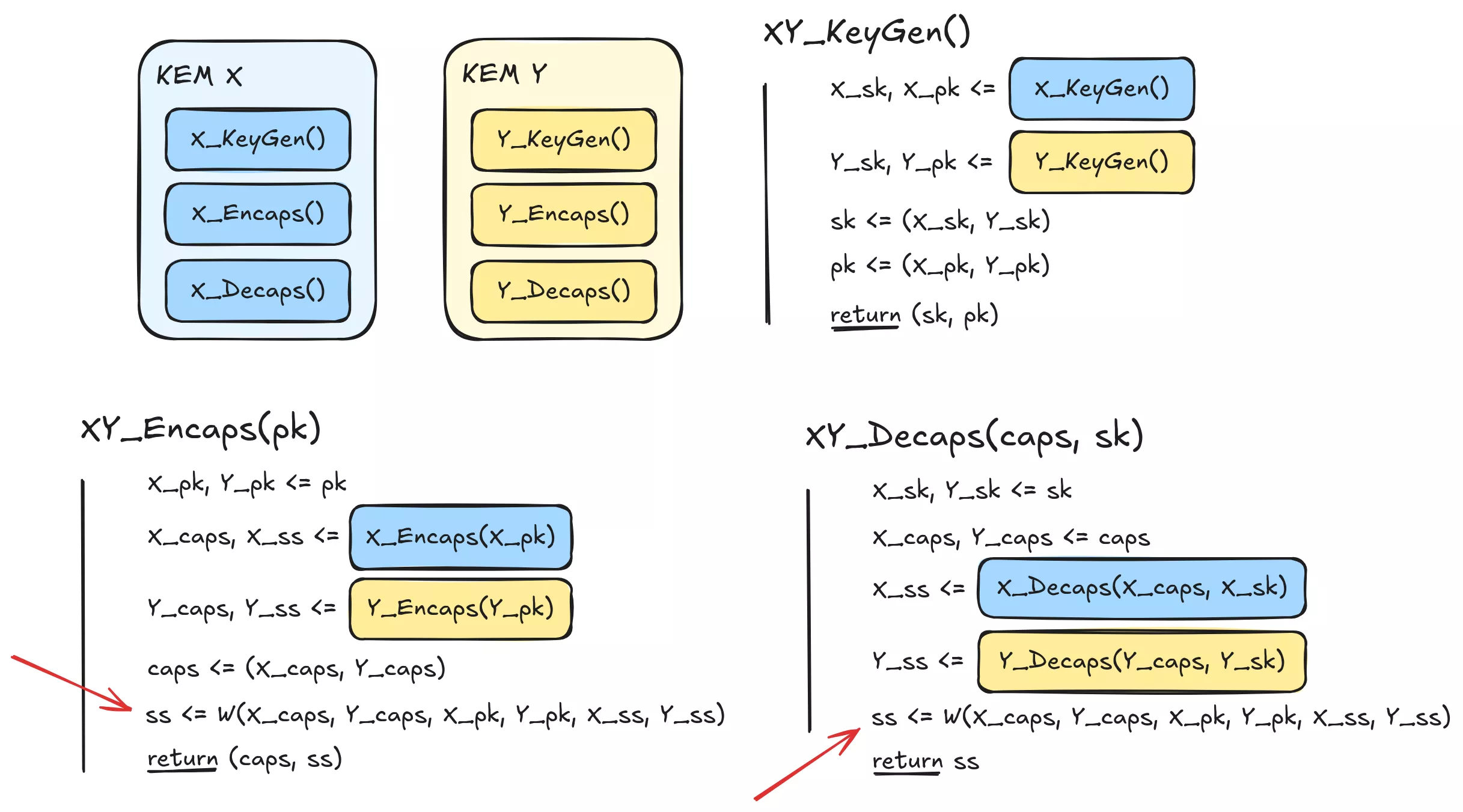
Dans les parties qui suivent, nous étudions de telles fonctions et nous donnons des éléments de compréhension sur les raisons pour lesquelles elles peuvent être ou non des choix pertinents.

Concaténer les secrets partagés

Une première approche pour combiner plusieurs secrets en un seul consiste simplement à tous les concaténer.

- CombiKEM.KeyGen():
    S_X, P_X <= KEM_X.KeyGen()
    S_Y, P_Y <= KEM_Y.KeyGen()
    S <= S_X, S_Y
    P <= P_X, P_Y
    return S, P

- CombiKEM.Encaps(P):
    P_X, P_Y <= Split(P)
    ss_X, caps_X <= KEM_X.Encaps(P_X)
    ss_Y, caps_Y <= KEM_Y.Encaps(P_Y)
    ss <= ss_X || ss_Y                 <--- W
    caps <= caps_X, caps_Y
    return ss, caps

- CombiKEM.Decaps(caps, S):
    caps_X, caps_Y <= Split(caps)
    S_X, S_Y <= S
    ss_X <= KEM_X.Decaps(caps_X, S_X)
    ss_Y <= KEM_Y.Decaps(caps_Y, S_Y)
    ss <= ss_X || ss_Y                 <--- W
    return ss

Cependant, cette approche n’est pas idéale pour plusieurs raisons :

• la longueur du secret partagé final varie en fonction du nombre de KEM combinés et de la taille de leurs sorties ;
• si l’un des KEM venait à être cassé, le secret partagé final serait partiellement connu d’un attaquant. De ce fait, il ne serait plus entièrement « secret ».

Idéalement, le fait de casser tous les KEM composants sauf un ne devrait pas donner suffisamment d’informations à un attaquant pour deviner des parties du secret partagé final. Intuitivement, un bon combineur doit diffuser l’entropie que chaque KEM apporte sur l’ensemble des bits du secret partagé final.

Concaténer les secrets partagés, puis hacher le résultat

En s’appuyant sur les leçons précédentes concernant la diffusion d’entropie, étudions une seconde proposition :

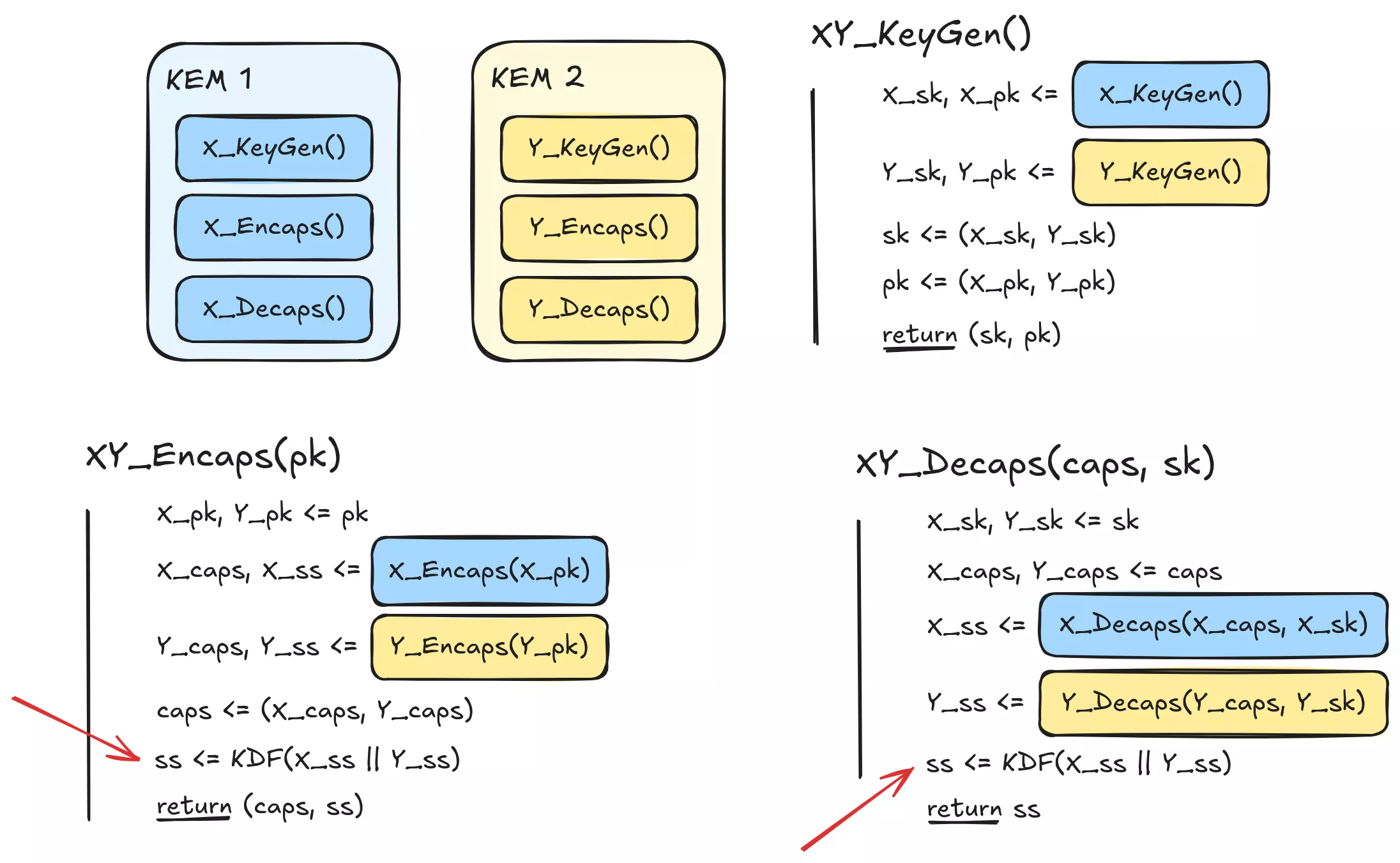
Ce combineur concatène l’ensemble des secrets partagés puis effectue une opération de dérivation de clé (par exemple avec une fonction de hachage) pour former le secret partagé final. Cela garantit que chaque bit de sortie dépend de chaque bit d’entrée. Cependant, dans un monde où notre combineur idéal doit être « au moins aussi bon » que chaque KEM qui le compose, cela reste insuffisant.

Pour prouver ce point, il est nécessaire de s’intéresser à la notion d’« indiscernabilité de la clé de session » (discutée dans deux papiers de l'IACR3 4). Elle décrit la capacité pour un adversaire de distinguer un secret partagé d’un blob aléatoire, étant donné la capsule correspondante.

L’indiscernabilité de la clé de session peut être vue comme un jeu consistant à deviner ce qui se cache dans une boîte, étant donné deux réponses possibles.

Deux niveaux d’indiscernabilité de la clé de session sont à distinguer :

• Indiscernabilité face aux attaques à clair choisi (IND-CPA) : Le challengeur fournit une clé publique, une capsule, son secret partagé associé et un blob aléatoire. L’adversaire a accès à un oracle d’encapsulation (Encaps) qu’il peut appeler autant de fois qu’il le souhaite, avec n’importe quelle clé publique de son choix. Après un nombre arbitraire d’appels à l’oracle, l’adversaire doit décider lequel des blobs fournis est le secret partagé encapsulé par la capsule fournie.
• Indiscernabilité face aux attaques à chiffré choisi (IND-CCA) : Le challengeur fournit toujours une clé publique, une capsule, son secret partagé associé et un blob aléatoire. L’adversaire a maintenant accès à un oracle d’encapsulation (Encaps(P)) et de décapsulation (Decaps(caps)) (la décapsulation étant effectuée avec la même clé que le challenge), qu’il peut appeler autant de fois qu’il le souhaite, sur n’importe quelle entrée sauf la capsule du challenge. Après un nombre arbitraire d’appels aux oracles, l’adversaire doit décider lequel des blobs fournis est le secret partagé encapsulé par la capsule fournie.

Pour reprendre notre métaphore du jeu de la boîte, l’IND-CPA est un jeu dans lequel l’adversaire a accès à une machine à emballer les cadeaux, permettant d’emballer autant d’objets qu’il le souhaite avant de devoir deviner ce que contient la boîte d’origine. L’IND-CCA donne accès à une machine pour emballer et déballer les cadeaux, à laquelle l’attaquant peut tout demander, sauf de déballer la boîte d’origine.

La sécurité d’un KEM peut être qualifiée vis-à-vis de cette propriété de sécurité, et notre combineur doit atteindre le même niveau d’indiscernabilité de la clé de session que le meilleur KEM qui le compose.

Malheureusement, le combineur « concaténer puis hacher » ne répond pas à ces attentes dans le cas général. En effet, considérons deux KEM, KEM_X et KEM_Y. Supposons de plus que KEM_X est IND-CCA sécurisé, mais que KEM_Y est afffaibli de telle manière qu’il est possible de trouver des collisions capsule/secret partagé pour une clé privée k fixe (mais secrète), c’est-à-dire que pour une certaine caps, on peut trouver caps′ ≠ caps tel que Decaps(caps,k) =  = Decaps(caps′,k). On note que KEM_Y n’est pas IND-CCA sécurisé ; étant donné un challenge (caps,s_A,s_B), un adversaire peut générer une capsule caps′ qui entre en collision avec caps puis interroger l’oracle de décapsulation avec Decaps(caps′). L’adversaire peut alors gagner le jeu en utilisant le secret partagé retourné par l’oracle.

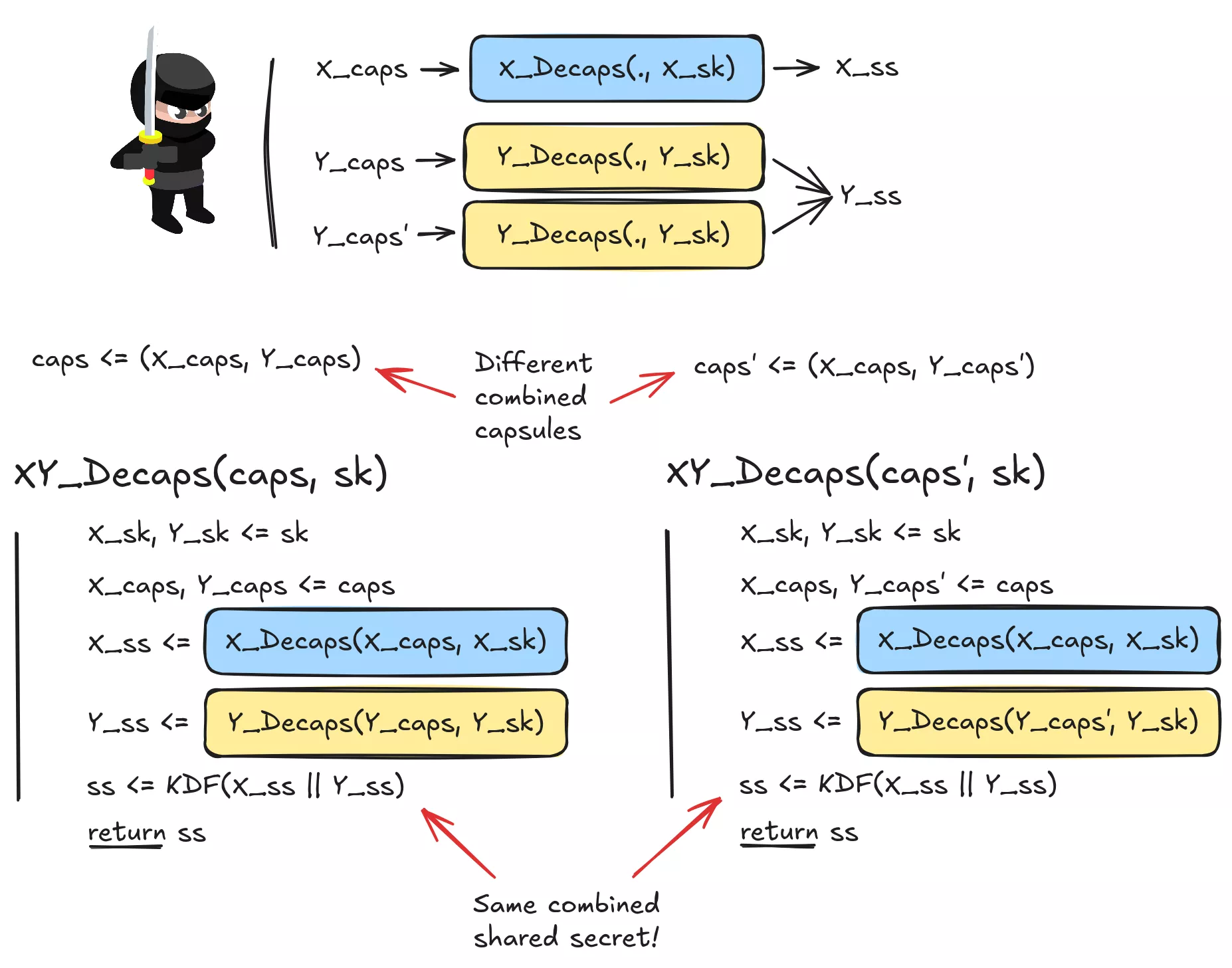
En effet, lorsqu’on lui fournit un challenge (caps,s_A,s_B) (où caps est composée de X_caps provenant de KEM_X et de Y_caps provenant de KEM_Y), l’adversaire est capable de fabriquer Y_caps′ ≠ Y_caps qui se décapsule avec KEM_Y en le même secret partagé. Ainsi, l’adversaire dispose de deux capsules différentes caps = X_caps, Y_caps et caps′ = X_caps, Y_caps′ qui se décapsulent avec le combineur en le même secret partagé. Avec le même argument que celui montrant que KEM_Y n’est pas IND-CCA, le combineur n’est pas IND-CCA alors que KEM_X l’est.

Notons qu’un KEM avec des collisions, comme KEM_Y dans la démonstration précédente, peut être instancié avec un échange de clés Diffie-Hellman dont les paramètres sont maladroitement choisis :

# === DH params
p=1277723 # p = 2*q + 1, avec q=638861 aussi un nombre premier
g=3       # ordre(g) = q


# === KeyGen()
# Clé privée d'Alice
a = 130376
# Clé publique d'Alice
A = pow(g, a, p)


# === Encaps(A)
# Clé privée éphémère de Bob
b = 644734
# Clé publique éphémère de Bob
B = pow(g, b, p)
# Secret partagé et capsule
ss, caps = pow(A, b, p), B


# === Decaps(caps, a)
assert pow(caps, a, p) == ss

# === Collision !
# Autre capsule, collisionnant avec caps (construite en utilisant le fait que `a` est pair)
v = 1277722    # order(v) = 2
caps_coll = (caps*v) % p
assert caps != caps_coll and pow(caps_coll, a, p) == ss

Comme vous pouvez le voir, pour une capsule donnée et une clé privée mal choisie, une seconde capsule qui entre en collision avec la première peut être trouvée instantanément dans ce schéma.

Néanmoins, selon M. Barbosa et al. 5, une combinaison « concaténer puis hacher » est sécurisée si l’on peut prouver la résistance à la seconde pré-image du chiffré des KEM composants. Cette propriété n’était clairement pas respectée dans notre exemple, puisque KEM_Y a été spécifiquement conçu pour fournir des collisions, d’où la rupture de la sécurité IND-CCA du KEM résultant.

Concaténer les secrets partagés et les capsules, puis hacher le résultat

Pour le cas général, l’article de M. Campagna & A. Petcher de 20204 propose d’inclure les capsules et les clés publiques de chaque KEM à la combinaison. Cet ajout permet de se défendre contre l’attaque présentée dans le paragraphe précédent, car les secrets partagés finaux des capsules en collision seront désormais différents. Cependant, les capsules et les clés sont très grandes pour les algorithmes post-quantiques, cette construction s’accompagne donc d’une perte non-négligeable en performance, sous la forme d’une entrée plus grande pour l’appel à la fonction de dérivation de clé.

Pour éviter cet inconvénient en termes de performance, le draft de l’IETF « Composite ML-KEM »6 utilise l’argument de M. Barbosa évoqué précédemment. En prouvant que ML-KEM possède une résistance à la seconde pré-image du chiffré, ils peuvent omettre en toute sécurité sa capsule et sa clé publique de l’entrée de la KDF. Cette approche maintient la sécurité IND-CCA requise sans la pénalité de performance.

KemCombiner<KDF>(mlkemSS, tradSS, tradCT, tradPK, Domain) -> ss
[...]
    if KDF is "SHA3-256":
        ss = SHA3-256(mlkemSS || tradSS || tradCT || tradPK || Domain)

    else if KDF is "HMAC-{Hash}":
        ss = HMAC-{Hash}(key={0}, text=mlkemSS || tradSS || tradCT || tradPK || Domain)
        ss = truncate(ss, 256)
    
    return ss

Fonction de combinaison utilisée dans Composite ML-KEM (IETF). Domain est une constante utilisée pour indiquer quelle paire spécifique d’algorithmes a été combinée.

Ce qu’il faut retenir

L’hybridation des échanges de clés offre une voie prudente pour l’avenir, mêlant la sécurité éprouvée des algorithmes classiques à la pérennité offerte par les schémas post-quantiques. Cependant, cet article démontre que la méthode utilisée pour combiner ces schémas est tout aussi critique que les schémas eux-mêmes. Nous avons vu qu’une simple concaténation des secrets partagés est insuffisante, et que même une approche intuitivement valide de type « concaténer puis hacher » peut introduire de subtiles vulnérabilités.

Pour construire un KEM hybride véritablement résilient, il existe deux voies principales :

• Une construction générique, qui incorpore non seulement les secrets partagés mais aussi les capsules et les clés publiques de chaque KEM dans la fonction de dérivation de clé finale. C’est la voie la plus sûre, mais elle peut avoir un coût de performance significatif en raison de la grande taille des artéfacts post-quantiques.
• Une approche plus optimisée, comme celle adoptée par l’IETF pour le ML-KEM Composite, qui repose sur la preuve de propriétés de sécurité plus fortes pour les KEM composants, telles que la résistance à la seconde pré-image du chiffré. Cela permet une combinaison plus légère qui omet les capsules et clés post-quantiques du hachage, atteignant ainsi de hautes performances sans sacrifier la sécurité.

En conclusion, la conception de mécanismes hybrides sécurisés est une tâche minutieuse, que ce soit pour les signatures ou pour les échanges de clés. Des standards robustes ont été publiés par des organismes comme le NIST et l’IETF, sur lesquels les développeurs peuvent s’appuyer. Ces standards fournissent un modèle de confiance pour atteindre à la fois une haute sécurité et des performances pratiques, garantissant que les communications chiffrées restent confidentielles face à tous les adversaires, présents et futurs. Si vous implémentez ces nouvelles primitives cryptographiques dans vos produits, nous vous encourageons vivement à soumettre votre travail pour une évaluation : Synacktiv se fera un plaisir de vous accompagner dans ce processus.

• 1. https://www.synacktiv.com/publications/quantum-readiness-lattice-based-…
• 2. https://synacktiv.com/publications/transition-post-quantique-lhybridati…
• 3. a. b. https://eprint.iacr.org/2018/024.pdf
• 4. a. b. https://eprint.iacr.org/2020/1364.pdf
• 5. https://eprint.iacr.org/2024/039
• 6. https://datatracker.ietf.org/doc/draft-ietf-lamps-pq-composite-kem/