Quantum readiness: Introduction to Modern Cryptography
This article is the first of a series of articles regarding Post-Quantum Cryptography in 2024. It builds upon Synacktiv's 2021 article, "Is it post quantum time yet?", by presenting the evolutions that happened since then in the PQC world as well as various constructions that will be reused in the next articles. These articles will especially focus on giving the reader a good understanding of the attack surface one should consider when designing and implementing a PQC algorithm.
Vous souhaitez améliorer vos compétences ? Découvrez nos sessions de formation ! En savoir plus
Where are we in 2024?
NIST published the first winners of its PQC competition in 2022 1. A single Public Key Encryption algorithm (PKE), used as a Key Encapsulation Mechanism (KEM) and 3 signature schemes are therefore set to be standardized:
Mechanism |
Type |
Name |
FIPS draft |
|---|---|---|---|
| PKE/KEM | Lattice | CRYSTALS-KYBER | FIPS 203 |
| Signature | Lattice | CRYSTALS-Dilithium | FIPS 204 |
| Signature | Lattice | FALCON | To be published |
| Signature | Hash-based | SPHINCS+ | FIPS 205 |
On the same day that NIST published the PQC competition winners, the 4th and possibly last round of candidate schemes was announced, including 4 PKE/KEM schemes. Amongst these, the isogeny-based SIKE algorithm was broken by an attack published soon after 2. While the SIKE's construction was proven to be fundamentally flawed, this does not close the door for other isogeny-based constructions to be designed and submitted, though none are currently being considered in the NIST competition.
Common concepts and primitives
Ciphertext Indistinguishability
. an attacker (henceforth "adversary") gives a defender (henceforth "challenger") two arbitrary messages $m_0$ and $m_1$, the challenger chooses one by randomly selecting a bit $b \in \{0, 1\}$, encrypts $m_b$, and sends the ciphertext back to the adversary. If the adversary manages to recover $b$ (i.e. ), they win. An encryption scheme is said to be indistinguishable if the probability for the adversary to determine $b$ isn't significantly higher than one half ($\frac{1}{2}$). We call the adversary's "advantage" the surplus of probability above $\frac{1}{2}$ that an adversary has at winning the game. Intuitively, it means that if the adversary has a non-negligible advantage over guessing, they have found a way to learn some information about the ciphertext.
Indistinguishability under chosen plaintext attack
Amongst the various indistinguishability properties, indistinguishability under chosen plaintext attack, or simply IND-CPA, offers the most basic level of protection; it is the weakest indistinguishability property, the one we trust the less to hide information from an adversary. An explicative diagram is included thereafter the formal definition of the IND-CPA game. The adversary has access to an encryption oracle $\mathscr{O}_{Enc}$ i.e. they can ask the challenger to encrypt a polynomially-bounded number of messages before they send their two challenge messages $m_0$ and $m_1$. Note that this oracle access is unnecessary for asymmetric schemes since the adversary has the public key, meaning they can encrypt messages on his own. After receiving $Enc_k(m_b)$, where $k$ denotes the symmetric key, the adversary can optionally do oracle queries once again before sending his guess $b'$ of $b$. For symmetric encryption schemes, whether or not the adversary can do some queries after receiving the ciphertext is the difference between IND-CPA and IND-CPA2 (indistinguishability under adaptive chosen plaintext attack).
A security parameter (also called the "security level") of $n$ bits, hereunder referred as $1^n$, is roughly the $\log_2$ of the number of operations an adversary would have to do in order to break the scheme. For example, a cryptographic scheme with a security parameter of $256$ bits means that the adversary would have to compute $2^{256}$ operations in order to break it.
Let's define more formally the CPA indistinguishability game given an encryption scheme $\Pi = (Gen, Enc, Dec)$, where $Gen$ is the key generation algorith, $Enc$ the encryption algorithm, and $Dec$ the decryption algorithm. $Gen$ takes as input a security parameter of the form $1^n$, a bit-string of $n$ ones, and outputs $pk$, the public key, and $sk$, the secret key. If we denote the bit length of a message $m$ as $|m|$, we have:
$\mathbf{PubK^{CPA}_{\mathcal{A},\Pi}(n)}$ : \begin{align} 1. & \textbf{Challenger: } (pk, sk) \leftarrow Gen(1^n) \\ 2. & m_0, m_1 \leftarrow \mathcal{A}(pk) \text{ with } m_0, m_1 \in M \text{ and } |m_0|=|m_1| \\ 3. & \textbf{Challenger: } b \leftarrow \{0, 1\}; c^* \leftarrow Enc_{pk}(m_b) \\ 4. & b' \leftarrow \mathcal{A}(c^*) \\ 5. & \text{if } b' = b \text{ return 1 } \\ & \text{else return } 0 \end{align}
$\mathcal{A}$ is a probabilistic polynomial-time (PPT) algorithm that represents the adversary. In a symmetric encryption setup we would write $\mathcal{A}^{Enc_{k}(\cdot)}$ to signify that the algorithm $\mathcal{A}$ has access to an encryption oracle $\mathscr{O}_{Enc_k}$ that calls the $Enc_k$ function and returns the result to the adversary.
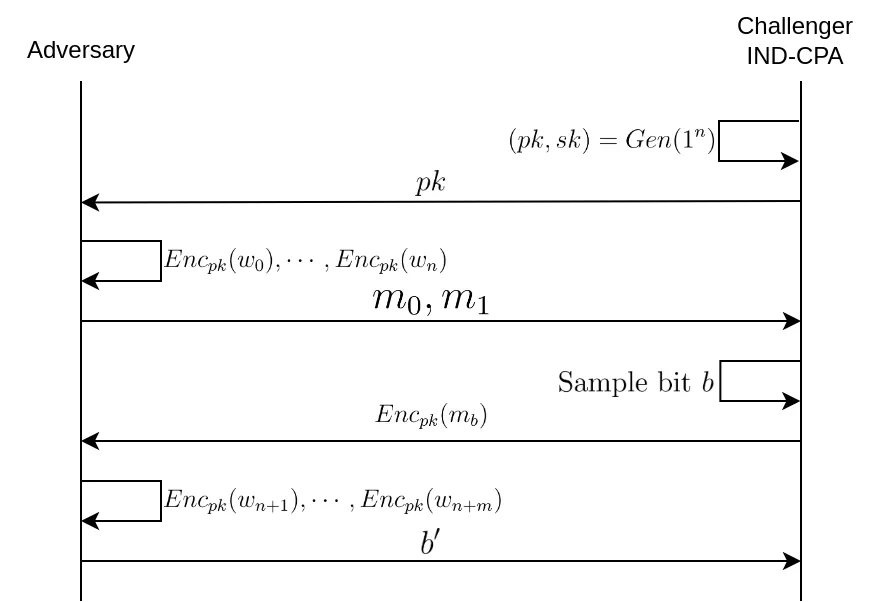
An asymmetric encryption scheme $\Pi$ is said to be IND-CPA if
\begin{align} Pr \left[ \mathbf{PubK^{CPA}_{\mathcal{A},\Pi}(n)} = 1 \right] \leq \frac{1}{2} + \epsilon(n) \end{align}
Where $\epsilon$, the adversary's advantage, is a negligible function i.e. for all polynomial $p$, there exists a $N \in \mathbb{N}$ such that for all $n > N$, $\epsilon(n) < \frac{1}{p(n)}$.
This definition conveys the idea that one of the best strategies that an adversary has for winning the IND-CPA game is tossing a coin, outputting $b' = 1$ if the coin lands on heads, $b' = 0$ otherwise.
For fun, let's prove that a deterministic encryption scheme cannot be IND-CPA:
Let $\Pi = (Gen, Enc, Dec)$ be a deterministic encryption scheme. To prove that $\Pi$ cannot be IND-CPA secure, we construct an adversary $\mathcal{A}$ that can win the IND-CPA game with probability $1$ (which is significantly greater than $\frac{1}{2}$).
- $\mathcal{A}$ begins by choosing two distinct messages $m_0 \neq m_1$ from the message space $M$.
- $\mathcal{A}$ sends $m_0$ and $m_1$ to the challenger.
- The challenger chooses a random bit $b \in \{0, 1\}$, encrypts $m_b$ using the deterministic encryption algorithm $Enc$, and sends the ciphertext $c^* = Enc_{pk}(m_b)$ back to $\mathcal{A}$.
- Since $\Pi$ is deterministic, the encryption of $m_0$ will always yield the same ciphertext $c_0 = Enc_{pk}(m_0)$, and similarly, $m_1$ will always be encrypted to $c_1 = Enc_{pk}(m_1)$. $\mathcal{A}$ can idependently encrypt $m_0$ and $m_1$ to determine if $c^* = c_0$ or $c^* = c_1$. If $c^* = c_0$, then $\mathcal{A}$ guesses $b' = 0$; otherwise, $\mathcal{A}$ guesses $b' = 1$.
- $\mathcal{A}$'s guess $b'$ will always be correct, as the deterministic nature of the encryption guarantees that the ciphertext $c^*$ can only correspond to one of the plaintexts $m_0$ or $m_1$. Thus, $\mathcal{A}$ wins the game with probability $1$.
Indistinguishability under chosen-ciphertext attack
Indistinguishability under chosen-ciphertext attack (IND-CCA) is a stronger notion that IND-CPA, meaning that IND-CCA wraps IND-CPA and also adds some security assurances. The IND-CCA game is similar to the IND-CPA game except that the adversary $\mathcal{A}$ has access to a decryption oracle $\mathscr{O}_{Dec_{sk}}$ on top of his encryption oracle (which is, once again, not explicited in the case of asymmetric cipher since the adversary has access to the public key, meaning they can encrypt messages himself).
$\mathbf{PubK^{CCA}_{\mathcal{A},\Pi}(n)}$ : \begin{align} 1. & \textbf{Challenger: } (pk, sk) \leftarrow Gen(1^n) \\ 2. & m_0, m_1 \leftarrow \mathcal{A}^{Dec_{sk}(\cdot)}(pk) \text{ with } m_0, m_1 \in M \text{ and } |m_0|=|m_1| \\ 3. & \textbf{Challenger: } b \leftarrow \{0, 1\}; c^* \leftarrow Enc_{pk}(m_b) \\ 4. & b' \leftarrow \mathcal{A}^{Dec_{sk}(\cdot)}(c^*) \text{ but } \mathscr{O}_{Dec_{sk}}(c^*) \text{ is prohibited } \\ 5. & \text{if } b' = b \text{ return 1 } \\ & \text{else return } 0 \end{align}
Similarly to the definition of IND-CPA security, we define the notion of IND-CCA security: \begin{align} Pr \left[ \mathbf{PubK^{CCA}_{\mathcal{A},\Pi}(n)} = 1 \right] \leq \frac{1}{2} + \epsilon(n) \end{align}
The difference between IND-CCA and IND-CCA2 (indistinguishability under adaptive chosen-ciphertext attack) is that, in the IND-CCA game, the adversary loses access to the decryption oracle after they sent $m_0$ and $m_1$, whereas in the IND-CCA2 they keep it after sending his messages. So IND-CCA2 is the strongest notion of the two.
Random Oracle Model
The Random Oracle Model (ROM) is a mathematical framework in which we assume the existence of random oracles. What's a random oracle you may ask? You can think of it as a deterministic black-box (something you can only interact with, not look inside) which, for each new input you give it, will output a completely random bit string. The "deterministic" part means that if you feed it an input you have previously supplied, it will output the same bit string it randomly sampled the first time. Random oracles are usually expressed as a function $H: \{0,1\}^* \rightarrow \{0,1\}^n$ taking an arbitrary-length bit string, and outputting a fixed-length bit string. The purpose of the ROM is to evaluate a cryptosystem that leverages the random oracle in order to obtain its security.
The problem is that real-life random oracles are impractical. You need to be able to store an exponential amount of input/output pairs elsewhere, and good luck finding a storage facility big enough to store more numbers as there are atoms in the observable universe, especially since the output numbers are completely random, there's no way of compressing them. So what? Are all cryptosystems proven to be secure in the ROM insecure in real life? Eh... no. What mathematicians do is that they come up with functions, called hash functions, that kinda behave like a random oracle, in the sense that an adversary has a negligible advantage in distinguishing the output of a mathematician's hash function from the output of the output of a true random oracle. One problem could be that a cryptosystem is secure in the ROM but becomes insecure whenever it is instanced with a real hash function, some even have been constructed as a proof of concept, but there hasn't been any real case of useful cryptosystem that was secure in the ROM but not in real case. So until we manage to get in touch with a real oracle, using the ROM as a basis for proofs is better than not proving anything at all.
Quantum Random Oracle Model
ROM proofs are pretty and all, but are they post-quantum secure? Meaning, is a cryptosystem proven to be secure in the ROM, also secure if the adversary makes quantum queries with a superposition over all inputs? Welcome to the wonderful world of quantum computing where you can input every possible inputs to a function in order to learn about every possible output. This is what Grover's search algorithm does. Given a function $f$ and an image $y$, it tries to find an $x$ such that $f(x) = y$. Instead of brute-forcing the whole input space, which is $\mathcal{O}(n)$, with $n$ possibly as huge as $2^{512}$, or even larger, in the case of cryptographic usages, Grover's algorithm superposes all possibles inputs of the function $f$, pass them through $f$, and search in just $\mathcal{O}(\sqrt{n})$ the input/output pair it wants. While Grover's search doesn't break any major cryptosystem, it severely weakens them by cutting by half their security level. So the major thing to be aware of is: if you want to use AES with the same security level against classical attacks that AES-128 has, but against quantum attacks, simply use AES-256.
Hash Functions
Cryptographic hash functions (henceforth "hash functions") are functions that take an arbitrary-length bit string as input and output a fixed-length bit string: $H: \{0,1\}^* \rightarrow \{0,1\}^n$. For example, for SHA3-256, $n = 256$. These hash functions must be:
- Collision-resistant: It should be computationally infeasible to find two different inputs that produce the same hash output.
- Preimage-resistant: Given a hash output, it should be computationally infeasible to find the original input.
- Second preimage-resistant: It should be difficult to find any second input that has the same hash output as a given input.
Like what was said before, we expect hash functions to behave like a random oracle. If a hash function $H$ behaves just like a random oracle, a corollary is that it becomes collision-resistant; i.e. if we define an adversary $\mathcal{A}$ who can make queries to the $H$ function, it has a very small probability of finding two distinct inputs $x$ and $y$ such that $H(x) = H(y)$:
\begin{align} Pr \left[ H(x) = H(y) \land x \neq y | (x, y) \leftarrow \mathcal{A}^{H(\cdot)} \right] \leq \mathcal{O}(\frac{q^2}{2^n}) \end{align}
With $q$ being the number of distinct queries the adversary $\mathcal{A}$ made to the function $H$.
The proof of this is quite brief :
- Since for every input $x$, $H(x)$ is a bit string of length $n$ independent of all other images of $H$, the probability of two images being the same is $\frac{1}{2^n}$;
- There are ${q \choose 2} = \mathcal{O}(q^2)$ input/output pairs found by the adversary.
Technically, an infinite number of collisions exist (the input domain is infinite and the output domain is finite, so hash functions can only be surjections), though they are hard to find. Say that your random function has $n = 256$ output bits, and that the adversary manages to bruteforce an astonishing $q = 2^{128}$ distinct queries, they have meagre chance of finding a collision of approximately $1.41 \times 10^{-73}$.
The Birthday Paradox
The Birthday Paradox is a probability puzzle that illustrates an interesting quirk of statistics: in a room of just 23 people, there’s a surprisingly high probability (over 50%) that at least two people will share the same birthday. This counterintuitive outcome arises from the fact that comparisons occur between every pair of individuals, greatly increasing the number of opportunities for a match, despite the number of people seeming relatively small.
This concept is directly applicable to the analysis of hash functions through what's known as the Birthday Attack. The paradox in the context of hash functions concerns the likelihood of two different inputs producing the same hash output, creating a collision. In the case of hash functions, the "birthday" is analogous to the hash value, and the "people" are the different input values. Suppose a hash function produces outputs that are $n$ bits long, which means there are $2^n$ possible hash values. Following the birthday paradox, we don't need to try all $2^n$ inputs to find a collision; rather, the number of inputs required to find a collision with a significant probability is about $\sqrt{2^n} = 2^{n/2}$. For a cryptographic hash function like SHA-256, which outputs 256 bits, the implication is that one only needs to try approximately $2^{128}$ different inputs to find a collision with some likelihood. This is far fewer than the $2^{256}$ inputs one might initially think necessary if considering each possible output individually. The feasibility of the birthday attack means that the security provided by hash functions is effectively halved.
The Birthday Attack can be further improved in the quantum world using the BHT algorithm that combines the Birthday Attack with Grover's algorithm, lowering to $\mathcal{O}(2^{n/3})$ the number of queries an adversary must make to order to find a collision.
The Fujisaki-Okamoto transform
The Fujisaki-Okamoto transformation 3 is a clever cryptographic technique that turns any IND-CPA (Indistinguishability under Chosen Plaintext Attack) secure public-key encryption scheme into an IND-CCA2 (Indistinguishability under Adaptive Chosen Ciphertext Attack) KEM (Key Encapsulation Mechanism). This transformation is particularly celebrated for its ability to fortify encryption schemes against more sophisticated attacks, without compromising on efficiency. It essentially acts as a security enhancer, making it a cornerstone in the development of robust cryptographic protocols. In fact, a lot of submissions to the call for Post-Quantum Cryptography Standardization from the NIST use the Fujisaki-Okamoto transform, in a form or another. CRYSTALS-Kyber (or just Kyber) is an example of KEM that uses the Fujisaki-Okamoto transform combined with Module Learning With Errors (M-LWE, a hard lattice problem that will be tackle with in a future post). It won the NIST competition for the first PQC standard in 2022.
Given an asymmetric encryption algorithm and a symmetric encryption scheme, FO does the following:
Encryption:
\begin{align} 1.\text{ }& r \leftarrow M \\ 2.\text{ }& k = G(r) \\ 3.\text{ }& c_m = Enc^{sym}_k(m) \\ 4.\text{ }& h = H(r, c_m) \\ 5.\text{ }& c_r = Enc^{asy}_{pk}(r; h) \\ 6.\text{ }& \text{return } c = (c_m, c_r) \end{align}
Recall that the asymmetric encryption scheme is IND-CPA so necessarily probabilistic. $Enc^{asy}_{pk}(\cdot; \cdot)$ denotes the deterministic variant of $Enc^{asy}_{pk}(\cdot)$, the parameter after the semicolon is used instead of the output to a query to a random oracle that would normally take place in the function.
Decryption:
\begin{align} 1.\text{ }& r' = Dec^{asy}_{sk}(c_r) \\ 2.\text{ }& h' = H(r', c_m) \\ 3.\text{ }& \text{if (} c_r \neq Enc^{asy}_{pk}(r'; h') \text{) return } \bot \\ 4.\text{ }& k' = G(r') \\ 5.\text{ }& \text{return } Dec^{sym}_{k'}(c_m) \end{align}
Security Proof
Proving that the Fujisaki-Okamoto transform is IND-CCA2 relies on a technique called game hopping. Simply put, you start with the game you want to evaluate (here the IND-CPA2 game) that's hard to evaluate, and "hop" from games to games that are more or less equivalent (not really but the adversary's advantage in succeeding in two consecutive games is tightly bounded) but somewhat easier to evaluate. Using game hopping, we show that if an adversary is able to win the IND-CPA2 game, we also are able to construct an adversary, sometimes called the extractor, that wins the CPA game by leveraging the answer of the IND-CPA2 adversary.
Alice is a CCA adversary attacking Bob, the CCA challenger.
The first difference (which corresponds to the first "game hop") with the normal CCA game is that Alice needs to make all of her random oracle queries to Bob. This doesn't change anything to the probability of Alice winning the game, this is only a conceptual change. The second game hop consists of creating Charlie, the CPA adversary that possesses the private key of the asymmetric encryption scheme, that Bob will attack.
We have Alice who is the IND-CPA2 adversary that is able to break the IND-CPA2 game, Bob which is the IND-CPA2 challenger and the CPA adversary, and Charlie which is the CPA challenger.
- Alice sends Bob her two messages $m_0$, $m_1$ to encrypt.
- Bob selects one at random (by uniformly sampling a random bit $b$).
- Bob samples two random values $r_0$, $r_1$ from the image space of $G$ and presents them to Charlie as its two input messages.
- Charlie samples $\bar{b}$ and encrypts $r_{\bar{b}}$ to produce $c^*_r$, and sends it to Bob.
- Bob then samples $k^*$, as in step 2 of encryption, as if $k^*$ was the image of $r_{\bar{b}}$ through $G$, except he doesn't know $r_{\bar{b}}$.
- Bob encrypts $m_b$ (the message he randomly chose from Alice) using the symmetric key $k^*$ in order to obtain $c^*_m$.
- Bob sends $c = (c^*_m, c^*_r)$ to Alice.
- Alice is forced to go through Bob's random oracles in order to correctly encrypt and decrypt messages.
- If Alice queries the random oracles with parameters that match those related to $r_0$ or $r_1$, whether it'd be to $G$ or $H$, Bob can deduce that Alice has succeeded in breaking the IND-CPA2 game, thereby identifying the value of $r_{\bar{b}}$ chosen by Charlie for encryption.
- Bob tells Charlie that he found $\bar{b}$, thereby succeeding the CPA game.
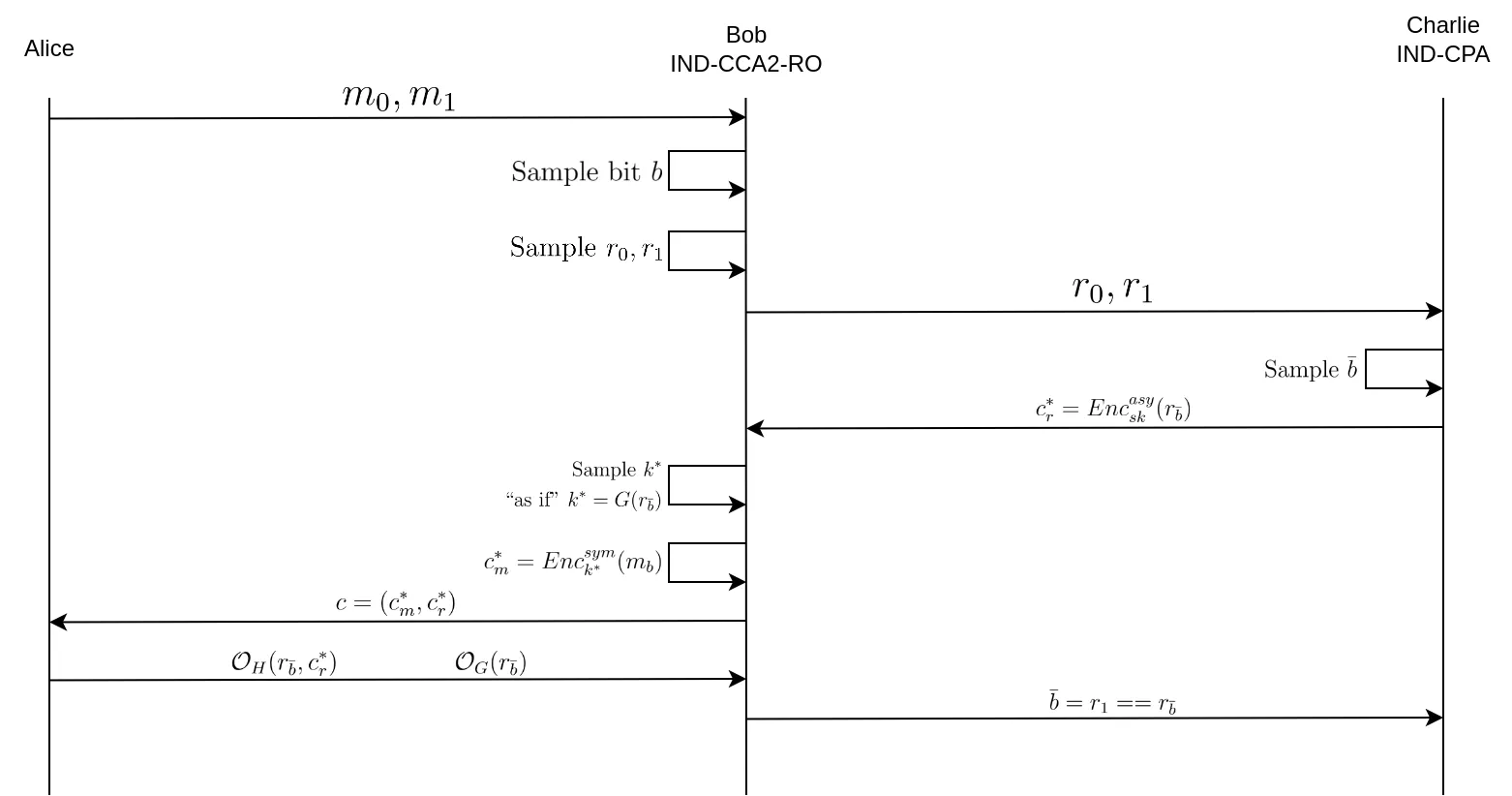
This is by no means a formal proof (for this I suggest reading the paper by Fujisaki and Okamoto linked in the footnotes) but more of an intuitive explanation of how the Fujisaki-Okamoto transformation achieves IND-CCA2 security from an IND-CPA asymmetric encryption scheme.
Zero-Knowledge Proofs
A Zero-Knowledge Proof (ZKP) is a method by which one party (the prover) can prove to another party (the verifier) that a certain statement is true, without conveying any additional information apart from the fact that the statement is true. The essence of zero-knowledge proofs lies in their ability to maintain absolute privacy of the underlying proof's details, which is not only intriguing from a theoretical standpoint but also invaluable in practical applications where sensitive information is involved.
A ZKP must satisfy three properties:
- Completeness: If the statement put forward by the prover is true, the honest verifier will be convinced by the honest prover.
- Soundness: If the statement is false, the honest verifier will find out that the prover cheated, except with negligible probability.
- Zero-Knowledge: If the statement is true, no verifier learns anything other than the fact that the statement is true.
In their most basic forms, ZKPs respect the Sigma Protocol (not an internet meme, it's a real crypto-thing). It typically consists of three steps:
- Commitment: The prover $P$ sends a commitment to the verifier, which is a value derived from the secret (the proof that the statement is true) but doesn't expose it.
- Challenge: The verifier $V$ sends a random challenge to the prover that only an actor with the secret can answer with a non-negligible probability (perhaps even 1).
- Response: $P$ computes a response to the challenge using the secret, and sends it to $V$.
$V$ can ask as many challenges to $P$ as they want until it is convinced that $P$ indeed has a true statement. A famous vulgarization of the sigma protocol is the Alibaba Cave.
Bob (the prover) wants to prove to Alice (the verifier) that he has indeed the secret passphrase of a magic door that lies inside a ring-shaped cavern.
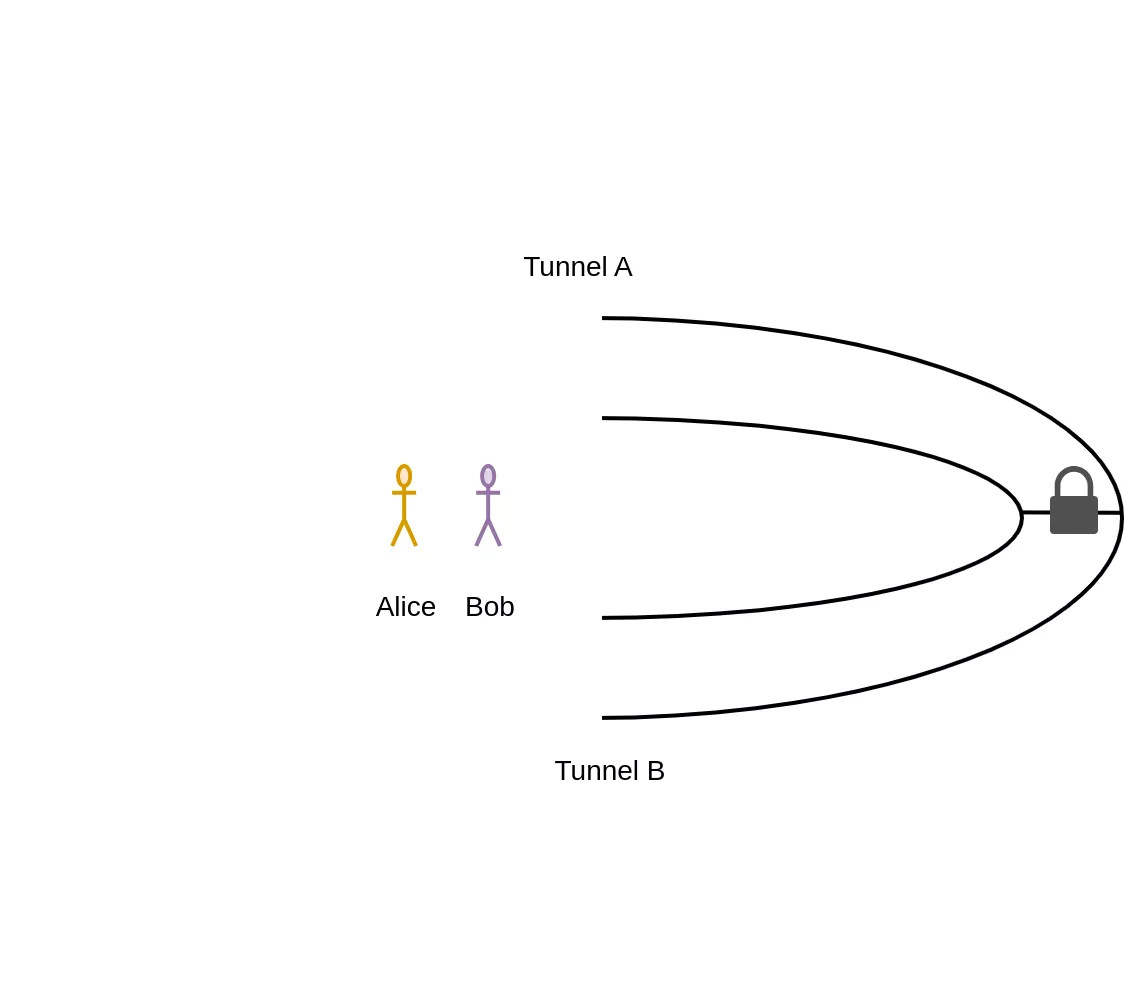
Bob asserts to Alice that he has the passphrase to the magic door at the end of the cavern, that's the commitment phase. Alice randomly chooses between A and B, and tells Bob which way should he go. If Alice picked A, Bob must enter the cavern by the tunnel A and exit the cavern by the tunnel B otherwise Alice will see that he lied on knowing the passphrase, and conversely, Alice will know that Bob lied if she picked B and Bob exits through the tunnel B instead of the tunnel A. She can repeat this process as many times as she like (maybe not until Bob's exhaustion). That's the challenge phase. Bob complies will Alice's request, that's the response phase.
Another well known ZKP example is for the Sudoku. In the commitment phase, Bob uses a permutation on the whole board to hide his solution and he makes a scratchcard off of it. Alice can then ask Bob to scratch off a column, a line, a square, or the original Sudoku. If Alice notices any errors in what Bob scratched off, it means he lied about having a solution. If Bob cheats, Alice has a probability of at least $\frac{1}{28}$ to find it out. But because she can ask Bob to remake a new scratch card with a new permutation each time, she progressively gains confidence that Bob indeed has a solution. After repeating this experiment 4000 times, Alice can be confident at approximately $99.\underbrace{9 \dots 9}_{\text{61 nines}}3348 \%$ that Bob doesn't lie.
Another type of scheme is the Fiat-Shamir heuristic. It allows to convert interactive ZKPs (such as the Sigma protocol) into non-interactive ZKPs in the ROM. Basically it consists of using a random oracle (think of "hash function" in real-world scenarios) to generate challenges instead of the verifier.
- Commitment: $P$ computes the initial commitment as in the interactive protocol.
- Challenge Generation: Instead of relying on $V$ to get a challenge, $P$ computes the hash of the initial commitment combined with any other relevant public data (this could include public keys, statements to be proved, or nonce values to ensure uniqueness). The output of the hash function serves as the challenge.
- Response Calculation: Using this hash-derived challenge, $P$ calculates the response exactly as they would in the interactive setting.
- Proof Assembly: $P$ packages the initial commitment, the hash-derived challenge, and the response into a single proof. This proof can be sent to the verifier or published in a public ledger for verification.
This scheme can also be used for message signature and authentication by embedding the signature data or the authentication data inside the commitment.
Conclusion
The outlined introductory concepts and mechanisms in post-quantum cryptography provide a foundational understanding of the current landscape and innovations in the field. As we navigate the complexities of securing cryptographic systems against quantum threats, these principles will serve as critical building blocks. Moving forward, we will delve deeper into these topics through a series of follow-up articles. Stay tuned for more detailed discussions and analyses in our upcoming publications.
- 1. NIST Announces First Four Quantum-Resistant Cryptographic Algorithms: https://www.nist.gov/news-events/news/2022/07/nist-announces-first-four…
- 2. An efficient key recovery attack on SIDH: https://eprint.iacr.org/2022/975.pdf
- 3. Fujisaki-Okamoto 2011: https://link.springer.com/content/pdf/10.1007/s00145-011-9114-1.pdf
